用级数展开避免0处发散

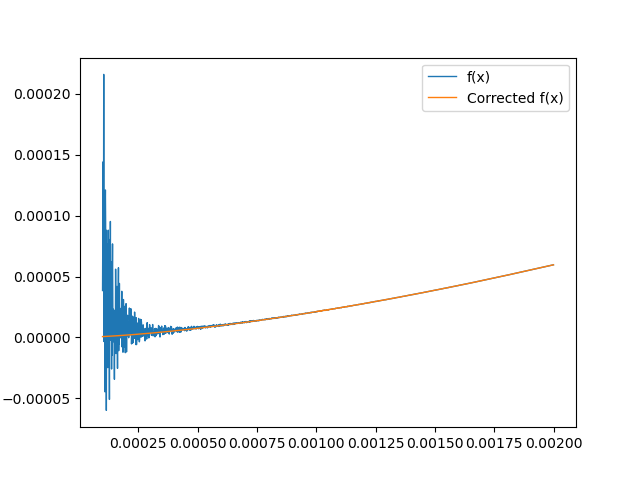
当函数的分母随自变量变换，绝对值越来越小时，函数可能会不稳定。在这种情况下，用级数展开来近似这个函数，可以避免这个问题。

例如，\( f(x)=\frac{\sqrt{1+x^3}}{x^{3/2}}-\frac{\ln [x^{3/2}+\sqrt{1+x^3}]}{x^3}\)在x趋近0时变化很大。要解决这个问题，首先把\( f(x)\) 在x=0处展开：

import sympy as sp
x = sp.Symbol('x')
print(((1+x**3)**.5/x**(3/2)- sp.log(x**(3/2)+(1+x**3)**.5)/x**3).series(x, 0, 5))

然后在x很小时，用这个展开来近似f(x)：

import numpy as np
import matplotlib.pyplot as plt
def f(x):
    if (x > 1e-3):
            return (1+x**3)**.5/x**(3/2)- np.log(x**(3/2)+(1+x**3)**.5)/x**3
    else:
        return -0.2*x**4.5 - 0.25*x**3.0 + 0.666666666666667*x**1.5 + 0.25*x**3
def f1(x):
    return (1+x**3)**.5/x**(3/2)- np.log(x**(3/2)+(1+x**3)**.5)/x**3 

a = np.arange(1e-4,2e-3,1e-6)
y=[]
for i in a:
    y_i=f(i)
    y.append(y_i)
plt.plot(a, f1(a), linestyle="-", linewidth=1,label="f(x)")
plt.plot(a, y, linestyle="-", linewidth=1,label="Corrected f(x)")
plt.legend()
plt.show()

比较如下图：