早期的宇宙是一个高温的等离子体,由自由电子、质子、原子核(主要是氦4核)和光子混合而成。电子与光子散射以及电子与原子核的库仑相互作用,使光子与物质之间达到热平衡。随着宇宙膨胀,温度降低,大约在温度低于3000K的时候(38万年),电子和质子结合成原子,叫做复合。光子几乎无法遇到自由电子(即光子解耦),光子两次相邻碰撞之间传播的平均距离变得很大。光子带着宇宙38万年时辐射涨落的信息传播,形成了我们看到的宇宙微波背景辐射(CMB)。CMB和绝对温标2.725K的黑体辐射相同。宇宙膨胀,光的波长越拉越长,宇宙温度越来越低,两者正好抵消,所以2.725K就是今天背景光子的温度。实际测量到的CMB温度在各个方向上有万分之一量级的起伏,在说明宇宙在大尺度下是均匀和各向同性的同时,也带给我们关于宇宙更小尺度结构的信息,后者是需要我们重点关注和挖掘的。
1,CMB各向异性的提取
首先将观测到的CMB减去全天平均温度,然后扣除相对于宇宙平均背景运动的偶极化影响,以及银河系中星体和尘埃的辐射影响,就得到了原始的各向异性CMB温度天图,如下图。
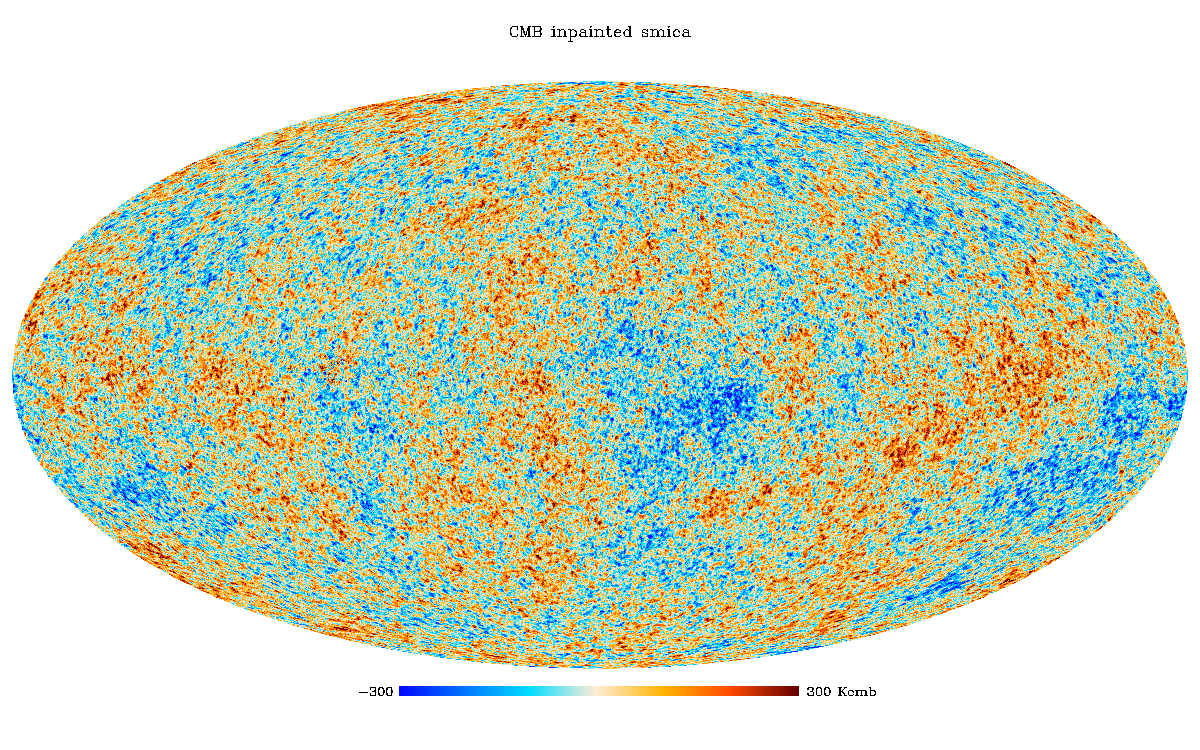
为了描述各向异性的统计特征,把天空CMB温度分布展开成球谐函数(Bond & Efstathiou,1987),并得到温度功率谱,如下图。
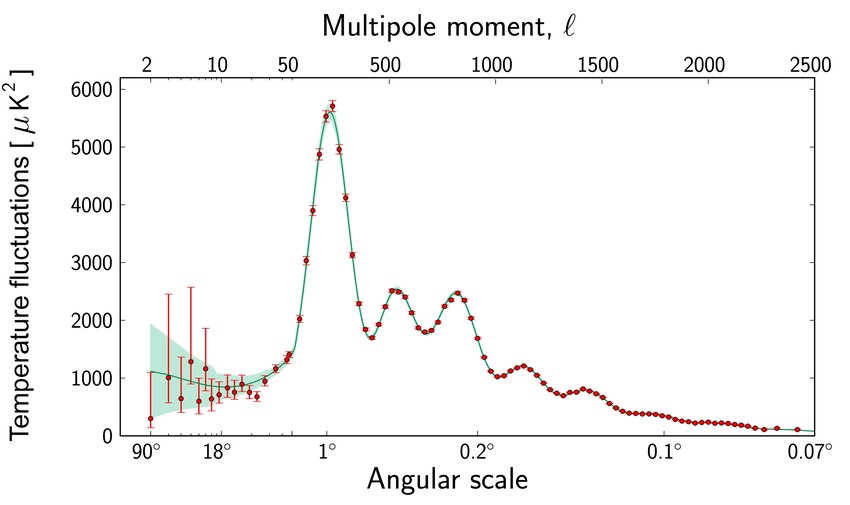
温度功率谱描绘了天空中两点之间温度的相关性。想象以某一张角在天图中取非常多对点。越多对点的两点温度接近,说明相关性越大,这个张角( 图二中的angular scale)对应的功率谱(图二中的纵坐标)值就越大。
2. 宇宙原初扰动对CMB的影响
在宇宙大爆炸前,暴涨使真空场产生微小不均匀性,引起物质密度涨落,叫做宇宙原初扰动。物质密度涨落引起引力势扰动。被压缩的地方温度更高,然而,这里的光子需要从更强的引力势阱中爬出,温度反而更低 ,这叫做SW效应。此时,还未进入视界的大尺度区域(angular scale>6度)只体现这个内禀因素,温度功率谱(即角功率谱)与原初密度扰动的物质功率谱相同。原初密度扰动的物质功率谱具有幂律形式:
\(\)$$\triangle^2(k)=A_s(k/k_p)^{n_s-1},$$
其中k_0是pivot_scale,一般取0.05Mpc-1。将平面波按贝塞尔函数展开,可以把物质功率谱换算成角功率谱C(l)
$$C^{SW}(l) \propto 2^{n_s-2}A_s(rk_0)^{1-ns}\frac{\Gamma(l+n_s/2-1/2)\Gamma(3-n_s)}{\Gamma(l+5/2-n_s/2)\Gamma^2(2-n_s/2)} \;\;\;\;(1)$$
其中r为光子解耦的共动距离。由上式可以看出,n_s等于1时,l(l+1)C^{SW}(l)是一个常数。改变n_s,l(l+1)C^{SW}(l)的变化如下图:
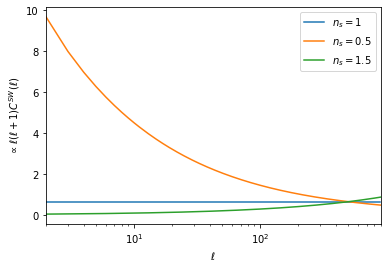
现在我们改变n_s,看看CMB温度功率谱的变化趋势:
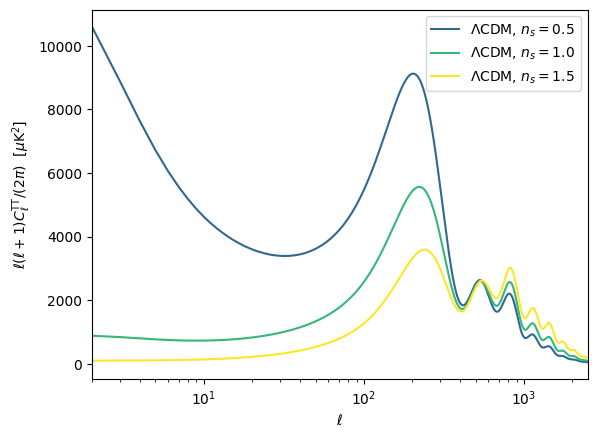
可以发现,ns控制了CMB温度功率谱整体的倾斜。在大尺度区域,CMB温度功率谱和C^{SW}(l)是基本一致的。此外,后边提到的积分SW效应还将对大尺度影响10%。
接下来,我们只改变A_s,如下图,A_s改变了整体的高度。这个从公式(1)也可以看出来。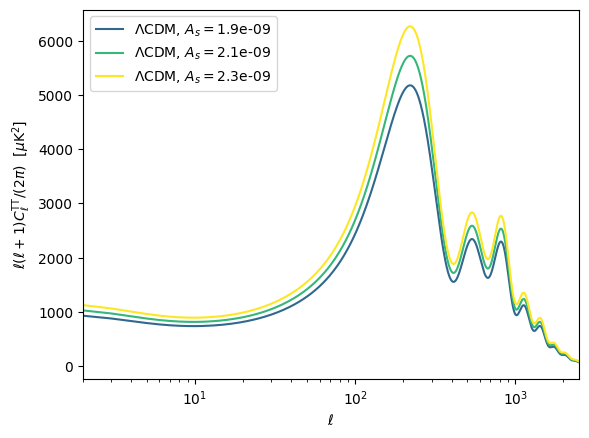
2,声学振荡
重子-光子等离子体在引力和光压的共同作用下不断疏密变化,形成纵波,这被称为声学振荡。光子在暗物质势阱与势垒中振荡,光子数目多的地方温度就相对较高。随着视界的增大,尺度从小到大的声学振荡依次进入视界,等离子体先是在引力的作用下收缩,然后在光压的作用下反弹,不断周期变化,直到氢复合之后,纵波冻结。
2.1 重子拖曳
CMB温度功率谱中的第1、3、5…个波峰对应在氢复合时刚好第1、2、3…次收缩完成,第2、4、6…个波峰则对应刚好第1、2、3…次反弹完成。在反弹时,重子的惯性作用使反弹无法完美完成,因此偶数峰比奇数峰更低。重子密度Ωbh^2越大,重子拖曳效应就越明显。重子密度增大还将导致引力作用变大,从而增大奇数峰的振幅(图?)。因此,第一个峰和第二个峰的比值对重子物质密度敏感。

2.2 暗物质
奇数峰不受重子拖曳效应的影响,为什么第三个峰没有第一个峰稿呢?在宇宙辐射主导时期,引力势能随着宇宙的膨胀而衰减,如果流体正好收缩完成准备反弹,衰减的引力势能使得光子爬出势阱消耗更少的能量,有效温度反号,功率谱增强。n=1模式在辐射主导时期开始了第一次(也是最后一次)的收缩,因此振幅增强。而对于n=3模式,尽管它比n=1更先开始振荡,但在最后一次收缩时,宇宙进入物质主导,因此受到这种驱动很小。如果减小暗物质密度Ωcdmh^2,宇宙推迟进入物质主导,n=1与n=3模式的差别将会缩小(图?)因此,第一个峰和第三个峰的比值对暗物质密度敏感。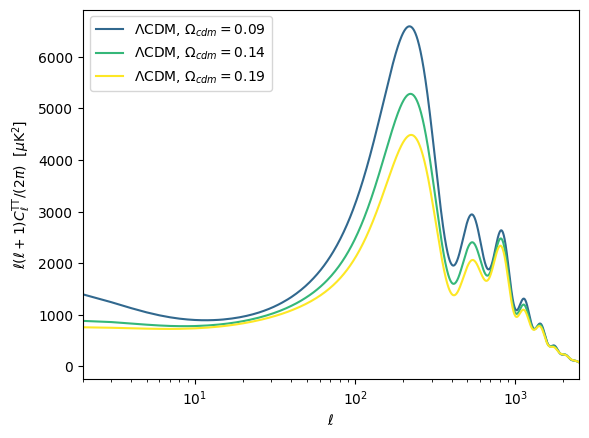
2.3 电子的多普勒效应
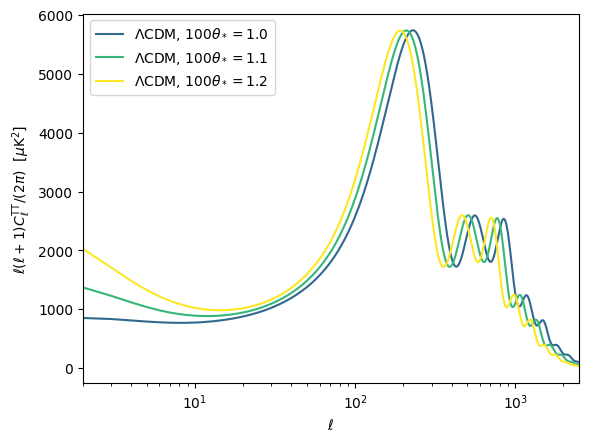
2.4声学视界第一个声学峰
3.光子的阻尼扩散
4.次级效应
5. 标准宇宙学的六个参数