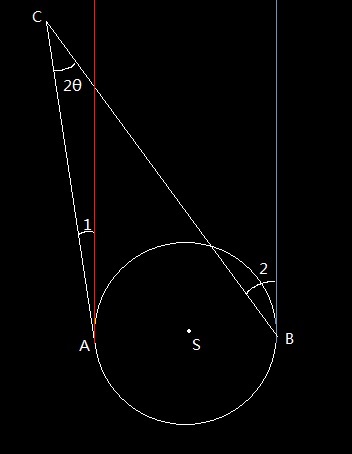
S是太阳,A和B是1月1日和7月1日地球的位置,AS=1Au(astronomical unit)。我们要测恒星C与我们的距离。
在1月1日测出角1,在7月1日测出角2,则他们的差的二分之一就是视差(parallax angle)(如果C处于两平行线之间,则角1和角2的和的二分之一就是视差),在上图中,视差就是角ACS也就是θ。
如何测角1和角2呢?假设上图是从北半球上空俯视的俯视图,而测量者在北半球。
地球在A时,选择日落时刻,则观察者朝正上方抬头看,视线延红线。然后再转一定角度朝向C,测出这个角度就是角1;半年后,地球在B,选择日出时刻,则观察者朝正上方抬头看,视线延蓝线。然后再转一定角度朝向C,测出这个角度就是角2。这样θ就求出来了。
由于C很远,视差很小,我们可以把AS近似看成角ACS对应圆弧,所以AC*θ=AS=1Au
即待测恒星的距离AC=1Au/θ 当视差θ=1″也就是1角秒时,AC=1秒差距(Pc),1Au=1.496*10^8km,1″=2π/(360*60*60)rad,1Pc=1Au/1″=30.856万亿千米。
more:

在实际操作中,
1.我们还要扣除天体的自行。这需要长期的跟踪才能将自行和周年视差区分开。
2.我们不用选择日出和日落,选一个遥远的天体,因为很遥远所以它在我们看来是固定不动的。想象上图的红线和蓝线都来自那个星体,那么角1和角2就是相隔半年的两个角距离,角距离在赤道坐标系上也可以体现出来。
举一个例子:2009年VLBA用三角视差测量银河系中心(银心)的距离的方法。
这个例子包含了我自己的理解,可能有误导的地方,希望大家看了文献后,告诉我下面的理解对不对。
人马座B2是位于银河系银心一个巨大的气体和尘埃分子云(很亮的恒星胎儿)。计算人马座B2的距离,就是银心的距离。
通过接收人马座B2的水分子脉泽,我们可以得到它的方位。选择J1745-2820作为背景参照(如图1),来得到人马座B2的真实移动(是方位的变化,不是真实速度),这里的真实移动是自行与周年视差的叠加。
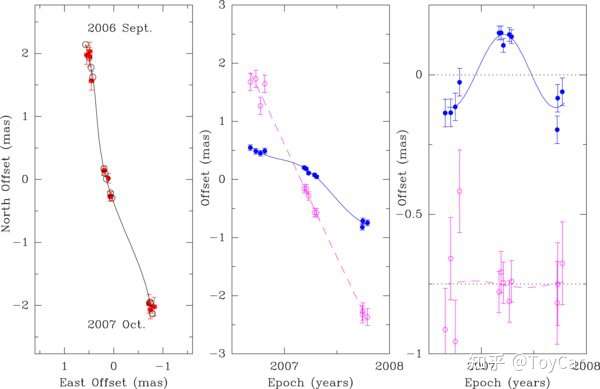
图二来自2006年9月到2007年10月测量
图二左,人马座B2相对与J1745-2820偏移的位置变化
图二中,向北偏移(粉色)和向东偏移(蓝色)随时间的变化
图二右,在图二中减去自行而得到的视差。
排除自行是很复杂的方法。他们的区别在于,视差是按年周期变化的,就像图二右那样,一年后回到原来的位置;而自行是沿着某个方向移动。
联星的自行可能比较好判断。在19世纪,W. Struve观察和筛选了很多双星的自行,包括织女星(联星),后来他得到了织女星的视差。