henon map

在Logistic map and henon map的结尾我简略地提到了henon映射。我今天写了一些相关的代码，就记录在这里吧。

研究二维映射之henon映射：\begin{cases}
x_{n+1}=1-ax_{n}^{2}+y_{n}\\
y_{n+1}=bx_{n}
\end{cases}
title=b=0.3，a=1.4时，每次迭代产生（x，y）的代码：

# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import numpy
import os
a=1.4
b=0.3
x,y=0.5,0.5
l=[]
os.chdir('D:\\py\\png')
for cut in range(50):#去除前一些点
x1=x
x=1-a*x**2+y
y=b*x1
for i in range(30000):
x1=x
x=1-a*x*x+y
y=b*x1
l.append([x,y])
l=numpy.array(l) 
plt.figure() 
plt.scatter(l[:,0],l[:,1],s=1,c="k",linewidths=0) 
plt.xlabel('x(n)') 
plt.ylabel('y(n)')
d='a='+str(a)+'_'+'b='+str(b)
plt.savefig(d+'.png')
plt.show()

现在可以用这些代码一探究竟了~~

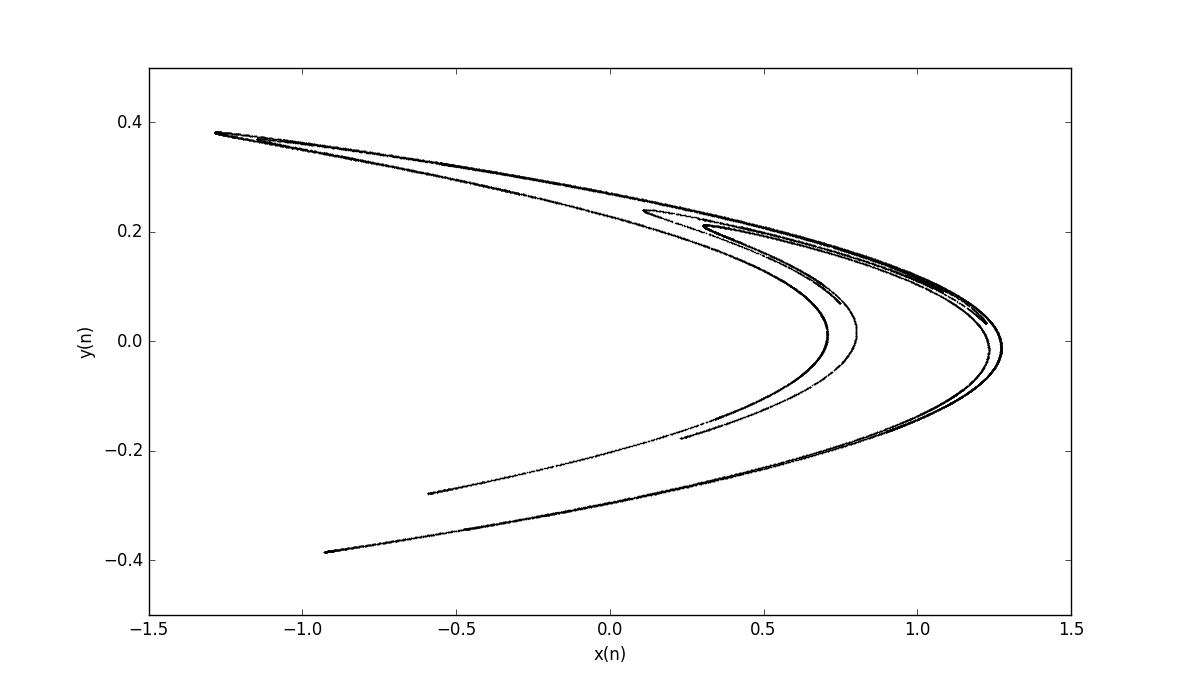
b=0.3，a=1.4

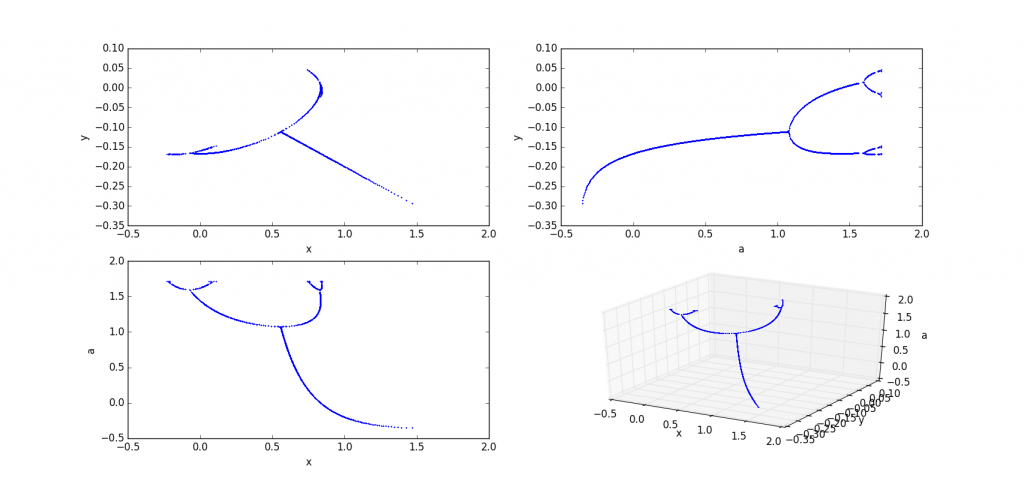
b=-0.2

拉到a的范围在1.6~1.8看看

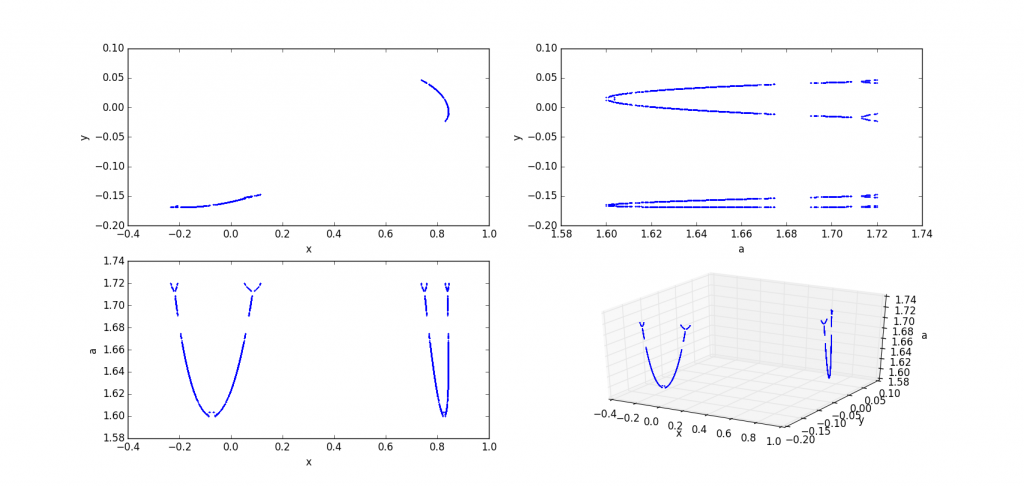
好像自相似唉。另外，有的a点并没有对应的（x，y）（计算机里的x，y的值是nan即Not a number）不知道是为什么。

b=0

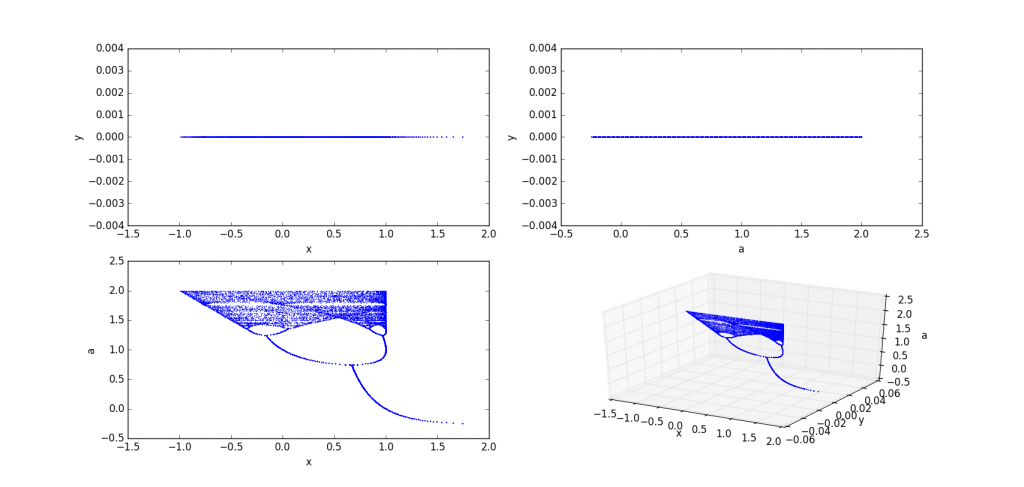
b=0.3

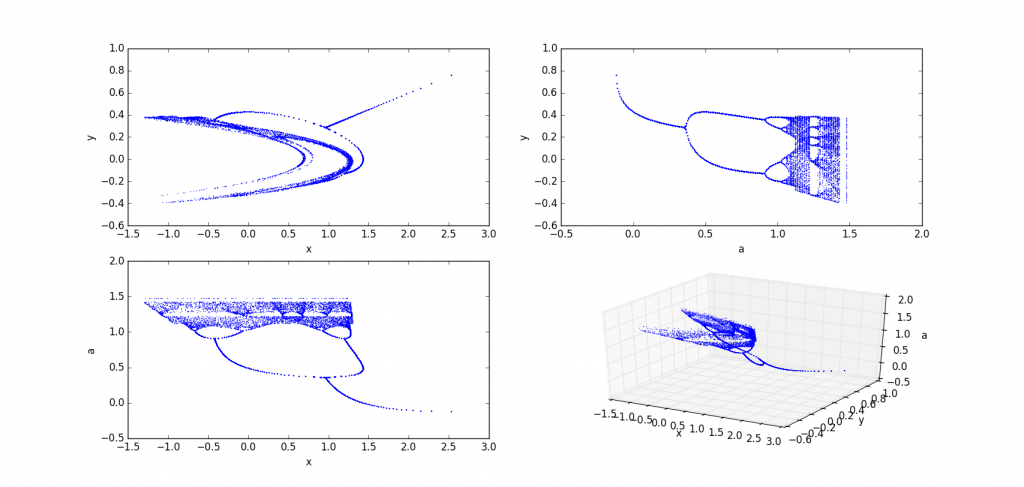
b=0.5

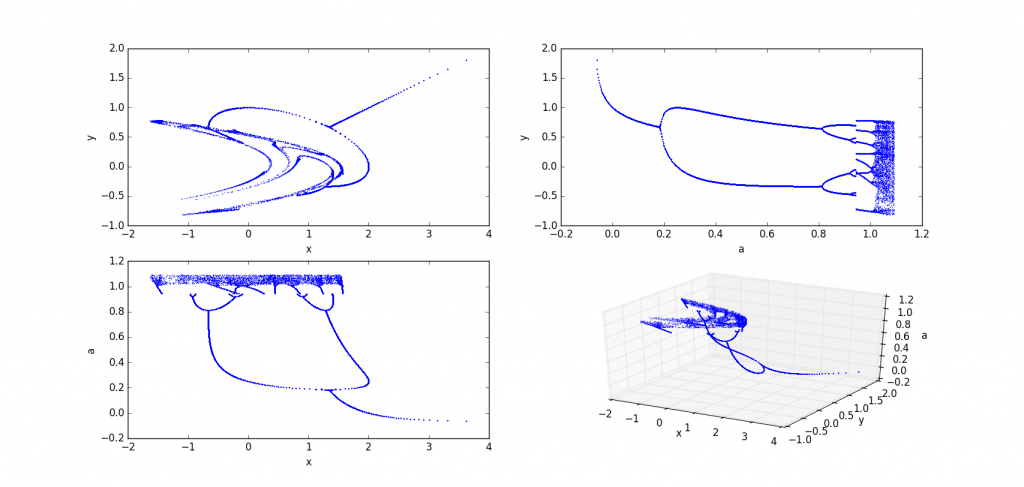
b=0.7

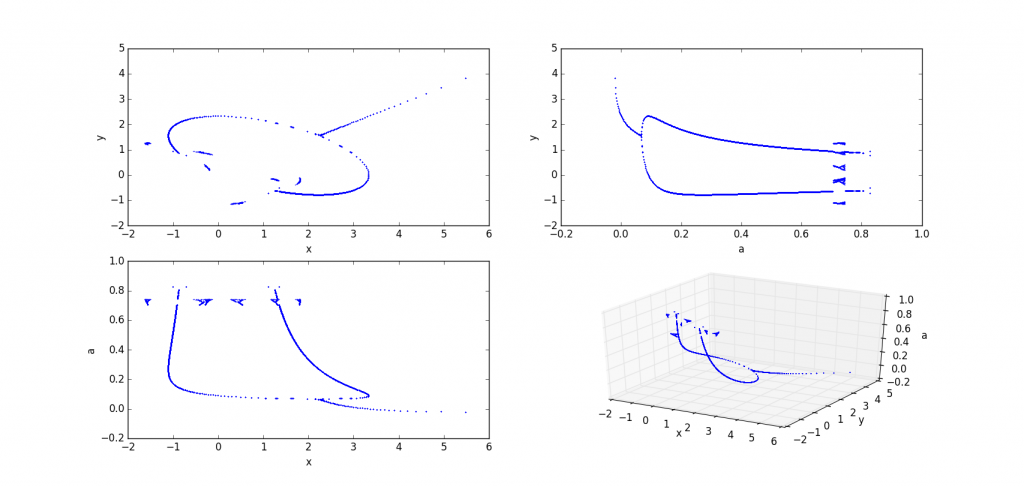
（图中发现，a取一些值（比如a=0.780）时没有对应的（x，y），计算机显示x和y为-inf即负无穷大。看来半路也有可能出叛徒呀）（后来我询问了老师，他用蛛网（cobweb）法给我解释了叛徒是怎么来的）

b=0.9

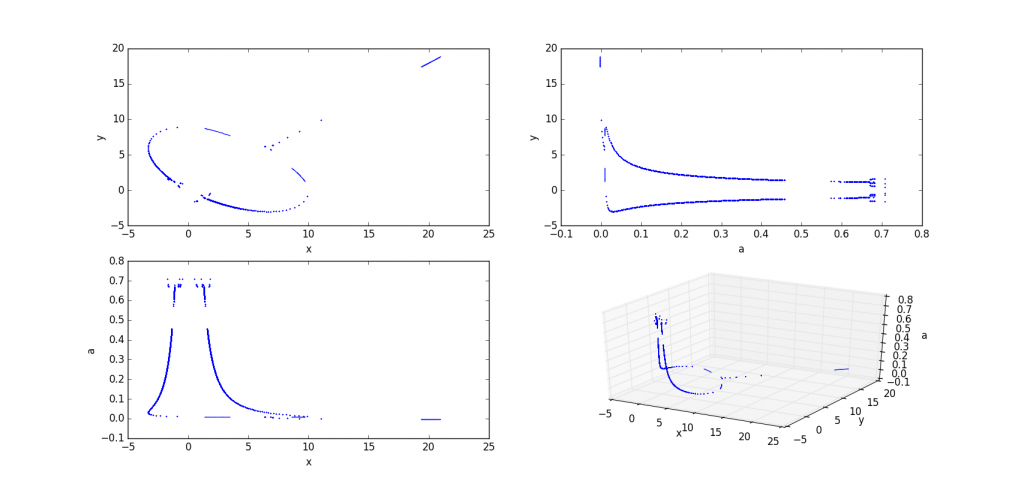
（半路也出了叛徒）

b=1

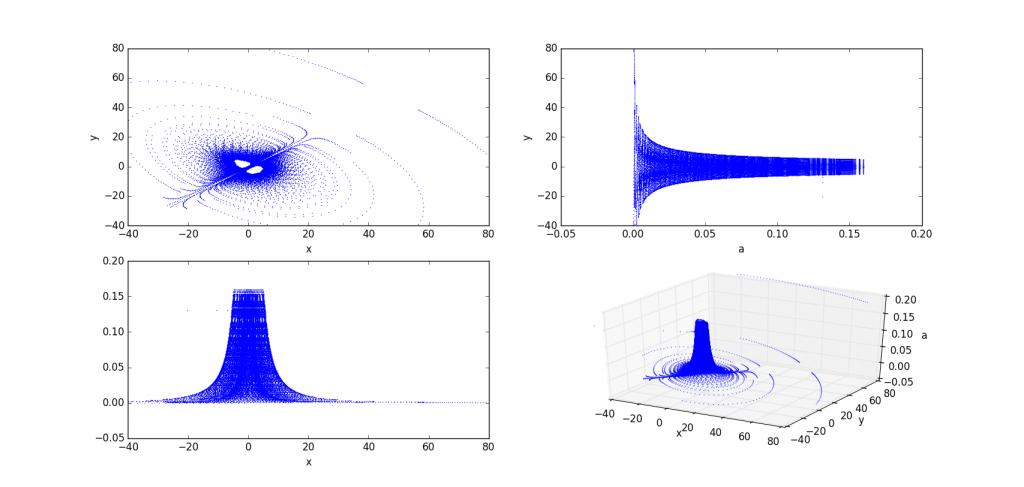
（这张图我对（x，y）的显示范围做了限制。因为x和y会跳到很大的值）

拉到局部看看。拉到a的范围在0.13~0.14

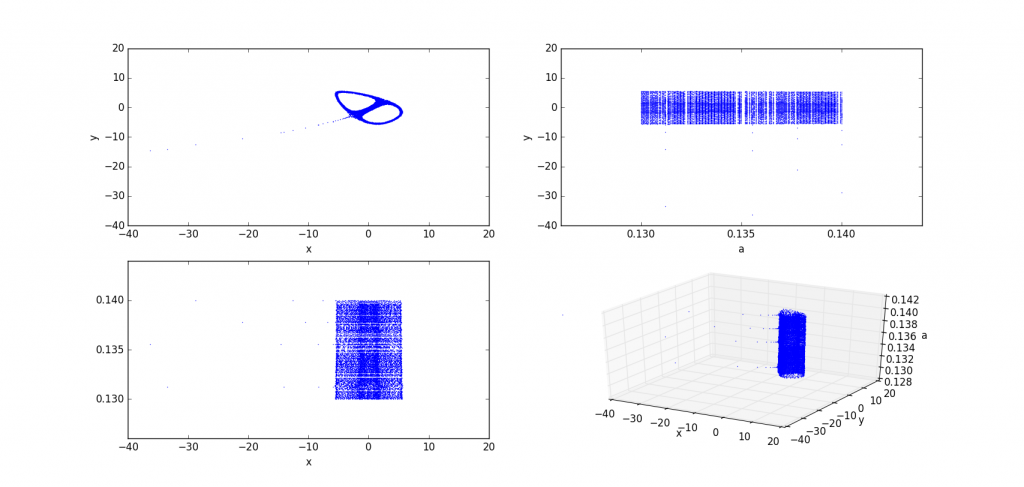
（这鼻孔的径向还拉丝呀）

a=0.3

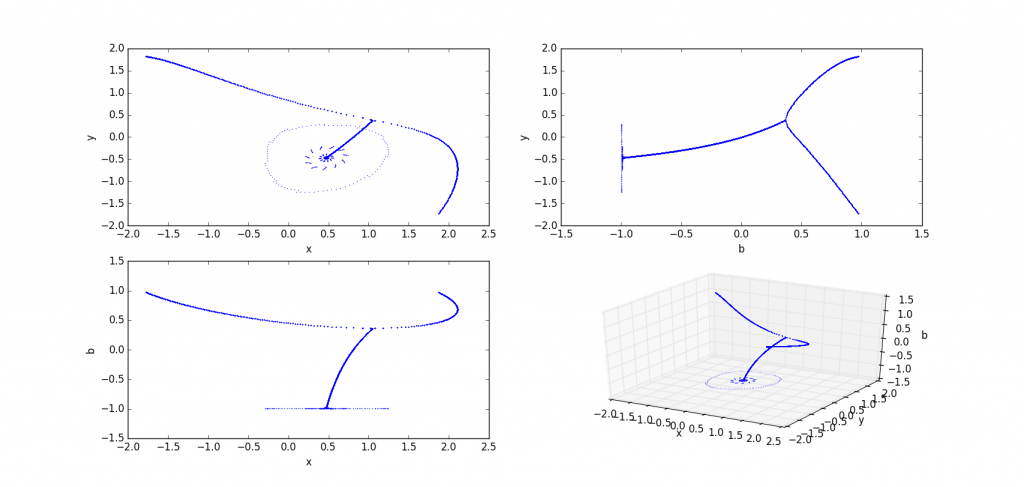
如果说上面那张是头顶风火轮，那么下面这张就是脚踏风火轮。可惜当时没有记录下a的值。我现在也懒得去找了。

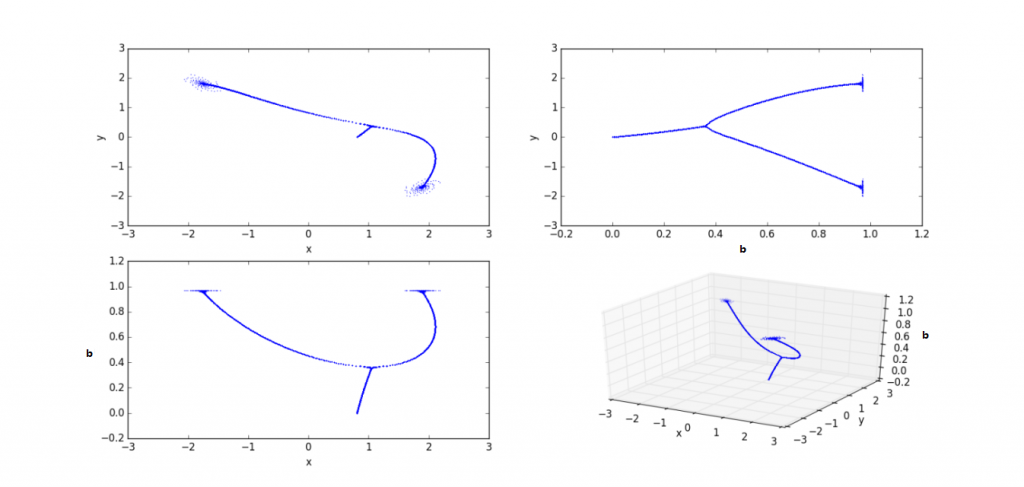
a=0.9

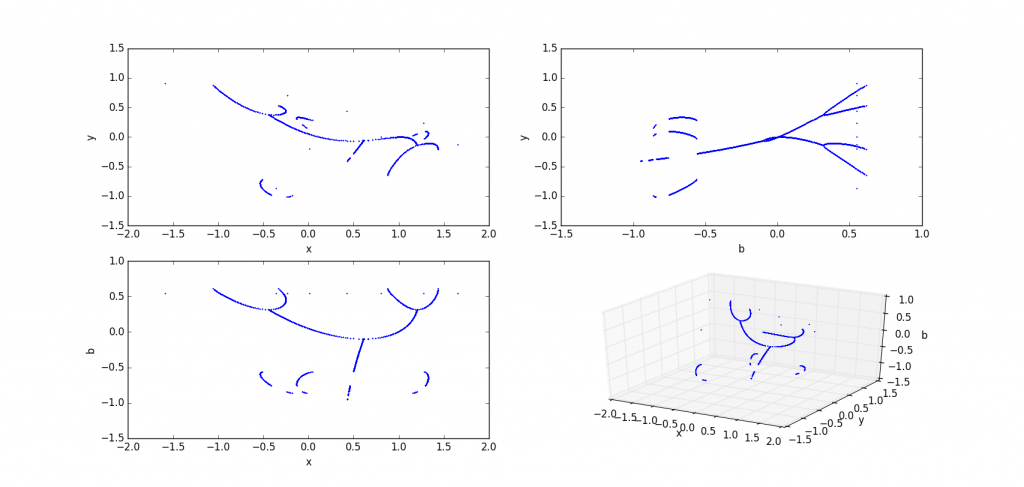
a=1.1

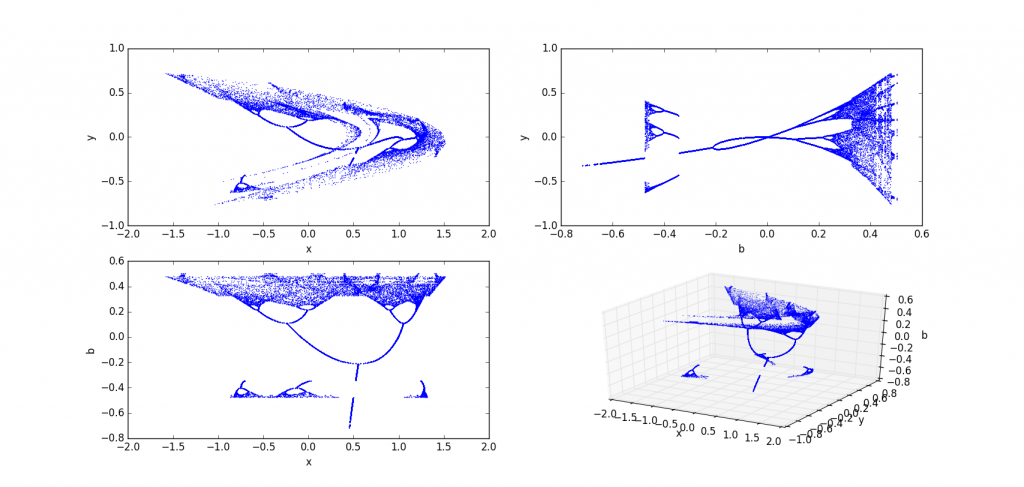
a=1.4

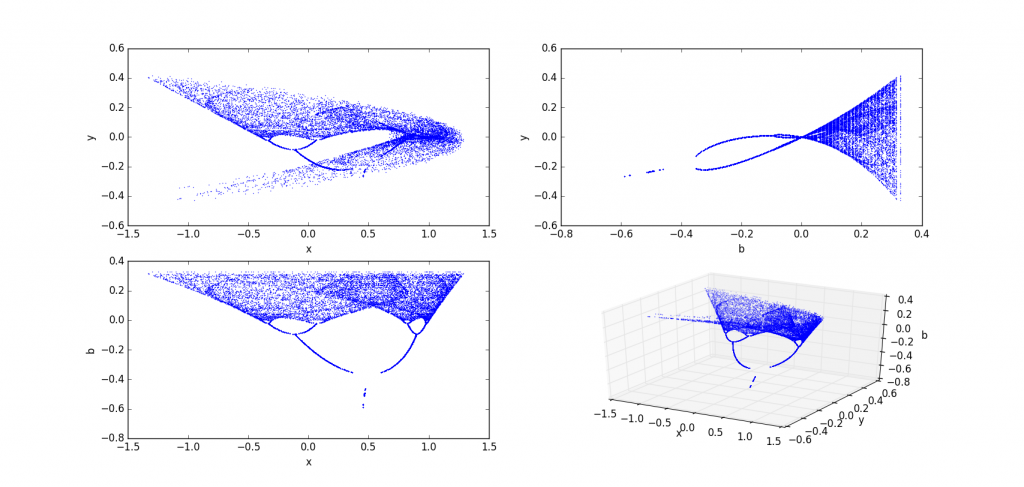
a=1.9

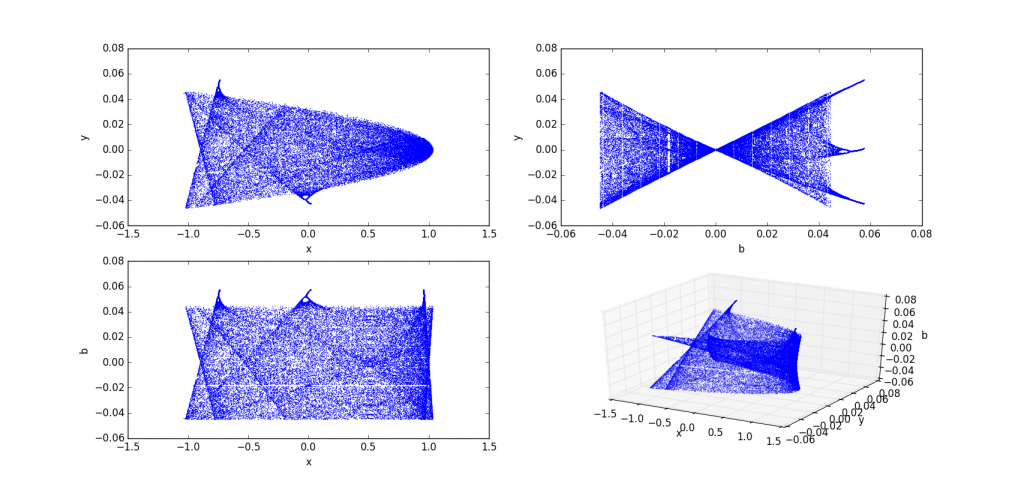
以上只是观看了四维怪物的三维投影，还没有开始进行研究。